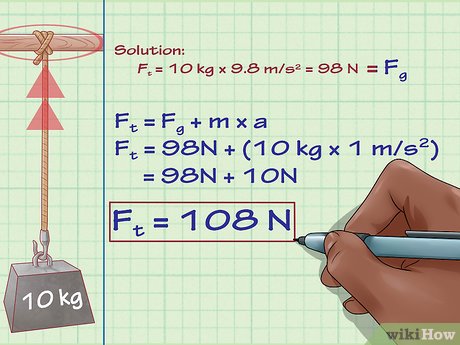Cách để Tính lực Căng dây trong Vật lý
Trong vật lý, lực căng dây là một lực được tạo ra bởi một sợi dây, sợi cáp hay các vật thể tương tự lên một hoặc nhiều vật khác. Bất cứ thứ gì khi được kéo, treo, trợ lực hay đung đưa trên một sợi dây đều sinh ra lực căng dây. Giống như các lực khác, lực căng dây có thể làm thay đổi tốc độ một vật hoặc làm biến dạng vật đó. Tính toán lực căng dây là một kỹ năng quan trọng không chỉ đối với học sinh chuyên ngành vật lý mà còn với các kỹ sư và kiến trúc sư, những người phải tính toán để biết liệu sợi dây đang dùng có chịu nổi sức căng của vật thể tác động không trước khi cho buông cần đỡ. Hãy đọc bước 1 để biết cách tính lực căng dây trong một hệ đa vật.
{“smallUrl”:”https://www.wikihow.com/images_en/thumb/3/3c/Calculate-Tension-in-Physics-Step-1-Version-3.jpg/v4-460px-Calculate-Tension-in-Physics-Step-1-Version-3.jpg”,”bigUrl”:”https://www.wikihow.com/images_en/thumb/3/3c/Calculate-Tension-in-Physics-Step-1-Version-3.jpg/v4-760px-Calculate-Tension-in-Physics-Step-1-Version-3.jpg”,”smallWidth”:460,”smallHeight”:345,”bigWidth”:760,”bigHeight”:570,”licensing”:”<div class=”mw-parser-output”></div>”}
1
Xác định lực căng ở 2 đầu sợi dây. Lực căng của sợi dây là kết quả của việc 2 đầu của nó phải chịu lực kéo. Nhắc lại công thức “lực = khối lượng × gia tốc. Giả sử sợi dây bị kéo rất căng, thì bất cứ thay đổi nào về trọng lượng hoặc gia tốc của vật đều làm lực căng dây thay đổi. Đừng quên yếu tố gia tốc gây ra bởi trong lực nhé – cho dù hệ vật có đang ở trang thái nghỉ đi nữa, thì mọi thứ trong hệ cũng vẫn sẽ phải chịu lực này. Ta có công thức lực căng dây T = (m × g) + (m × a), trong đó “g” là gia tốc do trọng lực của các vật trong hệ và “a” là gia tốc riêng của vật.
- Trong vật lý, để giải toán, ta thường đặt giả thuyết sợi dây ở “điều kiện lý tưởng” – tức là sợi dây đang dùng rất mạnh, không khối lượng hoặc khối lượng không đáng kể, và không thể đàn hồi hay đứt.
- Lấy ví dụ, xét một hệ vật gồm một quả nặng treo trên sợi dây như trong hình. Cả 2 vật đều không di chuyển vì đang ở trạng thái nghỉ. Vị thế, ta biết rằng với quả nặng đang nằm ở vị trí cân bằng, lực căng dây tác động lên nó phải bằng với trọng lực. Nói cách khác, Lực (Ft) = Trọng lực (Fg) = m × g.
- Giả sử khối lượng quả nặng là 10 k, giá trị lực căng dây là 10 kg × 9.8 m/s2 = 98 Newton.
- Giả sử khối lượng quả nặng là 10 k, giá trị lực căng dây là 10 kg × 9.8 m/s2 = 98 Newton.
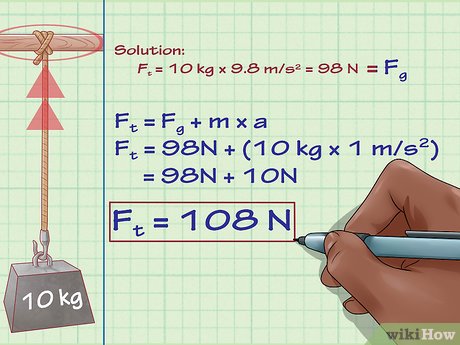
{“smallUrl”:”https://www.wikihow.com/images_en/thumb/d/d8/Calculate-Tension-in-Physics-Step-2-Version-3.jpg/v4-460px-Calculate-Tension-in-Physics-Step-2-Version-3.jpg”,”bigUrl”:”https://www.wikihow.com/images_en/thumb/d/d8/Calculate-Tension-in-Physics-Step-2-Version-3.jpg/v4-760px-Calculate-Tension-in-Physics-Step-2-Version-3.jpg”,”smallWidth”:460,”smallHeight”:345,”bigWidth”:760,”bigHeight”:570,”licensing”:”<div class=”mw-parser-output”></div>”}
2
Bây giờ ta tính thêm gia tốc vào. Trong lực không phải là tác nhân duy nhất ảnh hưởng tới lực căng dây, mọi lực khác liên quan đến gia tốc của vật mà sợi dây đang giữ cũng có khả năng như vậy. Lấy ví dụ, nếu ta tác động một lực làm thay đổi chuyển động của vật đang treo, lực gia tốc của vật đó (khối lượng × gia tốc) sẽ được thêm vào giá trị của lực căng dây.
- Trong ví dụ của chúng ta: Cho một quả nặng 10 kg treo trên sợi dây, nhưng thay vì trước đó sợi dây được cố định vào xà gỗ thì bây giờ ta kéo sợi dây theo phương thẳng đứng với gia tốc 1 m/s2. Trong trường hợp này, ta phải tính thêm cả gia tốc của quả nặng cũng như trọng lực. Cách tính như sau:
- Ft = Fg + m × a
- Ft = 98 + 10 kg × 1 m/s2
- Ft = 108 Newtons.
- Ft = Fg + m × a
- Ft = 98 + 10 kg × 1 m/s2
- Ft = 108 Newtons.
{“smallUrl”:”https://www.wikihow.com/images_en/thumb/8/8f/Calculate-Tension-in-Physics-Step-3-Version-3.jpg/v4-460px-Calculate-Tension-in-Physics-Step-3-Version-3.jpg”,”bigUrl”:”https://www.wikihow.com/images_en/thumb/8/8f/Calculate-Tension-in-Physics-Step-3-Version-3.jpg/v4-760px-Calculate-Tension-in-Physics-Step-3-Version-3.jpg”,”smallWidth”:460,”smallHeight”:345,”bigWidth”:760,”bigHeight”:570,”licensing”:”<div class=”mw-parser-output”></div>”}
3
Tính thêm gia tốc quay. Một vật khi đang bị quay tròn quay một tâm cố định thông qua một sợi dây (ví dụ như quả lắc) sẽ sinh ra lực căng dựa trên lực hướng tâm. Lực hướng tâm cũng đóng vai trò bổ sung vào lực căng dây vì nó cũng “kéo” vật vào trong, nhưng ở đây thay vì kéo theo hướng thẳng thì nó lại kéo theo hình cung. Vật quay càng nhanh, lực hướng tâm càng lớn. Lực hướng tâm (Fc) được tính bằng công thức m × v2/r trong đó “m” là khối lượng , “v” là vận tốc và “r” là bán kính của đường tròn chứa cung chuyển động của vật.
- Vì hướng và độ lớn của lực hướng tâm thay đổi khi vật chuyển động, nên tổng lực căng dây cũng vậy, bởi lẽ lực này luộn kéo vật theo một hướng song song với sợi dây và hướng vào tâm. Ngoài ra bạn hãy nhớ trọng lực vẫn luôn đóng vai trò tác động theo phưởng thẳng đúng. Tóm lại, nếu một vật đang đung đưa theo phương thẳng thì lực căng của sợi dây sẽ đang cực đại tại điểm thấp nhất của cung chuyển động (với con lắc, ta gọi đó là vị trí cân bằng), khi mà ta biết rằng vật sẽ chuyển động nhanh nhất ở đó và châm nhất ở 2 biên.
- Vẫn lấy ví dụ về quả nặng và sợi dây, nhưng thay vì kéo thì ta cho quả nặng đung đưa như quả lắc. Giả sử sợi dây dài 1.5 mét và quả nặng chuyển động với vận tốc 2m/s khi nó ở vị trí cân bằng. Muốn tính lực căng dây trong trường hợp này, ta cần tính lực căng dây do trọng lực như khi nó không chuyển động là 98 Newton, sau đó tính lực hướng tâm thêm vào như sau:
- Fc = m × v2/r
- Fc = 10 × 22/1.5
- Fc =10 × 2.67 = 26.7 Newtons.
- Vậy tổng lực căng dây là 98 + 26.7 = 124.7 Newton.
- Fc = m × v2/r
- Fc = 10 × 22/1.5
- Fc =10 × 2.67 = 26.7 Newtons.
- Vậy tổng lực căng dây là 98 + 26.7 = 124.7 Newton.
{“smallUrl”:”https://www.wikihow.com/images_en/thumb/f/ff/Calculate-Tension-in-Physics-Step-4-Version-2.jpg/v4-460px-Calculate-Tension-in-Physics-Step-4-Version-2.jpg”,”bigUrl”:”https://www.wikihow.com/images_en/thumb/f/ff/Calculate-Tension-in-Physics-Step-4-Version-2.jpg/v4-760px-Calculate-Tension-in-Physics-Step-4-Version-2.jpg”,”smallWidth”:460,”smallHeight”:345,”bigWidth”:760,”bigHeight”:570,”licensing”:”<div class=”mw-parser-output”></div>”}
4
Bạn nên hiểu rằng lực căng dây sẽ khác nhau tại các vị trí khác nhau của vật trên cung chuyển động. Như đã nói ở trên, cả hướng và độ lớn của lực hướng tâm của vật sẽ thay đổi khi vật chuyển động. Tuy nhiên, mặc dù trọng lực vẫn không đổi, lực căng dây tạo ra bởi trọng lực vẫn sẽ thay đổi như thường! Khi vật ở vị trí cân bằng, trọng lực tác động sẽ theo phương thẳng đứng và lực căng dây cũng vậy, nhưng khi vật ở vị trí khác thì 2 lực này sẽ tạo với nhau một góc nhất định. Vì vậy, lực căng dây đã “trung hòa” một phần của trọng lực thay vì hợp toàn bộ.
- Chia lực hấp dẫn thành 2 vector sẽ giúp bạn thấy rõ hơn về định nghĩa này. Tại một điểm bất kỳ thuộc cung chuyển động của một vật theo phương thẳng đứng, sợi dây tạo ra một góc “θ” với đường đi từ tâm đến vị trí cân bằng của vật. Khi chuyển động, lực hấp dẫn (m × g) sẽ được chia ra làm 2 vector – mgsin(θ) tiệm cận với cung chuyển động hướng tới vị trí cân bằng. Và mgcos(θ) có phương song song với lực căng dây theo hướng ngược lại. Qua đó ta thấy lực căng dây chỉ phải chống lại mgcos(θ) – phản lực của nó – chứ không phải toàn bộ lực hấp dẫn (Ngoại trừ lúc vật ở vị trí cân bằng, các lực đó đều cùng phương và hướng).
- Bây giờ cho qua lắc tạo với phương thẳng đứng một góc 15 độ, chuyển động với vận tốc 1.5m/s. Vậy ta tính lực căng như sau:
- Lực căng dây tạo ra bởi trọng lực (Tg) = 98cos(15) = 98(0.96) = 94.08 Newton
- Lực hướng tâm (Fc) = 10 × 1.52/1.5 = 10 × 1.5 = 15 Newton
- Tổng lực = Tg + Fc = 94.08 + 15 = 109.08 Newton.
- Lực căng dây tạo ra bởi trọng lực (Tg) = 98cos(15) = 98(0.96) = 94.08 Newton
- Lực hướng tâm (Fc) = 10 × 1.52/1.5 = 10 × 1.5 = 15 Newton
- Tổng lực = Tg + Fc = 94.08 + 15 = 109.08 Newton.
{“smallUrl”:”https://www.wikihow.com/images_en/thumb/f/f5/Calculate-Tension-in-Physics-Step-5-Version-2.jpg/v4-460px-Calculate-Tension-in-Physics-Step-5-Version-2.jpg”,”bigUrl”:”https://www.wikihow.com/images_en/thumb/f/f5/Calculate-Tension-in-Physics-Step-5-Version-2.jpg/v4-760px-Calculate-Tension-in-Physics-Step-5-Version-2.jpg”,”smallWidth”:460,”smallHeight”:345,”bigWidth”:760,”bigHeight”:570,”licensing”:”<div class=”mw-parser-output”></div>”}
5
Tính thêm lực ma sát. Bất kỳ vật nào khi bị kéo đều sinh ra một lực “rê” bởi sự ma sát lên bề mặt của vật thể (hay chất lỏng) khác và lực này làm thay đổi phần nào lực căng dây. Lực ma sát của 2 vật trong trường hợp này cũng sẽ được tính theo cách chúng ta thường thực hiện : Lực mà sát (thường ký hiệu là Fr) = (mu)N, Trong đó mu là hệ số ma sát mà N là lực tạo ra bởi 2 vật, hoặc lực nén của vật này lên vật kia. Lưu ý mà sát tĩnh khác với ma sát động – ma sát tĩnh là kết quả của việc làm cho một vật từ trạng thái nghỉ sang chuyển động còn ma sát động sinh ra khi duy trì cho một vật tiếp tục chuyển động của nó.
- Giả sử ta có một quả nặng 10 kg nhưng giờ nó bị kéo lê trên sàn theo phương ngang. Cho hệ số ma sát động của sàn là 0.5 và quả nặng ban đầu có vận tốc không đổi nhưng bây giờ ta thêm cho nó gia tốc 1 m/s2. Vấn đề mới này có 2 sự thay đổi quan trọng – Thứ nhất, ta không còn tính lực căng do trọng lực nữa, vì bây giờ lực căng dây và trọng lực không triệt tiêu nhau. Thứ hai, ta phải thêm lực ma sát và gia tốc. Cách tính sẽ như sau :
- Lực thông thường (N) = 10 kg × 9.8 (gia tốc trọng lực) = 98 N
- Lực ma sát động (Fr) = 0.5 × 98 N = 49 Newton
- Lực gia tốc (Fa) = 10 kg × 1 m/s2 = 10 Newton
- Tổng lực căng dây = Fr + Fa = 49 + 10 = 59 Newton.
- Lực thông thường (N) = 10 kg × 9.8 (gia tốc trọng lực) = 98 N
- Lực ma sát động (Fr) = 0.5 × 98 N = 49 Newton
- Lực gia tốc (Fa) = 10 kg × 1 m/s2 = 10 Newton
- Tổng lực căng dây = Fr + Fa = 49 + 10 = 59 Newton.
{“smallUrl”:”https://www.wikihow.com/images_en/thumb/c/c4/Calculate-Tension-in-Physics-Step-6-Version-2.jpg/v4-460px-Calculate-Tension-in-Physics-Step-6-Version-2.jpg”,”bigUrl”:”https://www.wikihow.com/images_en/thumb/c/c4/Calculate-Tension-in-Physics-Step-6-Version-2.jpg/v4-760px-Calculate-Tension-in-Physics-Step-6-Version-2.jpg”,”smallWidth”:460,”smallHeight”:345,”bigWidth”:760,”bigHeight”:570,”licensing”:”<div class=”mw-parser-output”></div>”}
1
Dùng ròng rọc để kéo một kiện hàng theo hướng song song. Ròng rọc là một loại máy cơ đơn giản bao gồm một đĩa tròn có tác dụng thay đổi hướng của lực. Trong một hệ ròng rọc đơn giản, sợi dây hay cáp chạy lên trên ròng rọc rồi lại đi xuống, tạo thành một hệ 2 dây. Tuy vậy, cho dù có đang kéo vật nặng với cường độ nhứ thế nào đi nữa thì lực căng của 2 “sợi dây” đều bằng nhau. Trong một hệ gồm 2 vật nặng và 2 sợi dây như vậy, lực căng dây bằng 2g(m1)(m2)/(m2+m1), trong đó “g” là gia tốc trọng trường, “m1” là khối lượng vật 1, và “m2” là khối lượng vật 2.
- Lưu ý, thông thường trong vật lý ta sẽ áp dụng “ròng rọc lý tưởng” – không khối lượng hoặc khối lượng không đáng kể, không ma sát, ròng rọc không hỏng hóc hoặc rơi khỏi máy cơ. Giả định như thế sẽ dễ tính hơn nhiều.
- Ví dụ ta có 2 quả nặng treo thẳng đứng trên 2 dây ròng rọc. Quả nặng 1 nặng 10 kg, quả 2 nặng 5 kg. Lực căng dây được tính như sau:
- T = 2g(m1)(m2)/(m2+m1)
- T = 2(9.8)(10)(5)/(5 + 10)
- T = 19.6(50)/(15)
- T = 980/15
- T = 65.33 Newtons.
- Lưu ý, bởi vì có một quả nặng và một quả nhẹ, hệ vật sẽ chuyển động, quả nặng đi chuyển hướng xuống và quả nhẹ thì ngược lại.
- T = 2g(m1)(m2)/(m2+m1)
- T = 2(9.8)(10)(5)/(5 + 10)
- T = 19.6(50)/(15)
- T = 980/15
- T = 65.33 Newtons.
2
Dùng ròng rọc để kéo một kiện hàng theo hướng không song song.Thường thì ta dùng ròng rọc để điều chỉnh hướng của vật đi lên hay đi xuống. Những nếu, một quả nặng đang được treo thẳng đúng ở một đầu dây, quả nặng kia nằm trên một mặt phẳng nghiêng, thì bây giờ ta sẽ có một hệ ròng rọc không song song bao gồm ròng rọc và hai quả nặng. Lực căng dây lúc này sẽ có thêm tác động đến từ trọng lực và lực kéo trên mặt phẳng nghiêng.
- Cho quả nặng treo thẳng đứng nặng 10 kg (m1) và quả nặng trên mặt phẳng nghiêng nặng 5 kg (m2), mặt phẳng nghiêng tạo với sàn một góc 60 độ (giả sử mặt phẳng có ma sát không đáng kể). Để tính lực căng dây, trước hết hãy tìm phép tính lực chuyển động của các quả nặng:
- Quả nặng treo thẳng nặng hơn và vì ta không tính đến lực ma sát, cho nên hệ vật sẽ chuyển động đi xuống theo hướng quả nặng đó. Lực căng dây lúc này sẽ tác động kéo nó lên, vì thế lực chuyển động sẽ phải trừ đi lực căng dây: F = m1(g) – T, or 10(9.8) – T = 98 – T.
- Ta biết rằng quả nặng trên mặt phẳng nghiêng sẽ bị kéo lên. Vì ma sát đã bị loại trừ, lực căng dây kéo quả nặng lên và chỉ có sức nặng của quả nặng kéo nó xuống lại. Thành phần kéo quả nặng xuống ta đặt là sin(θ). Vậy trong trường hợp này, ta tính được lực kéo quả nặng là: F = T – m2(g)sin(60) = T – 5(9.8)(.87) = T – 42.63.
- Gia tốc của 2 vật là bằng nhau, ta có (98 – T)/m1 = T – 42.63 /m2. Từ đó tính được T = 79.54 Newton.
- Quả nặng treo thẳng nặng hơn và vì ta không tính đến lực ma sát, cho nên hệ vật sẽ chuyển động đi xuống theo hướng quả nặng đó. Lực căng dây lúc này sẽ tác động kéo nó lên, vì thế lực chuyển động sẽ phải trừ đi lực căng dây: F = m1(g) – T, or 10(9.8) – T = 98 – T.
- Ta biết rằng quả nặng trên mặt phẳng nghiêng sẽ bị kéo lên. Vì ma sát đã bị loại trừ, lực căng dây kéo quả nặng lên và chỉ có sức nặng của quả nặng kéo nó xuống lại. Thành phần kéo quả nặng xuống ta đặt là sin(θ). Vậy trong trường hợp này, ta tính được lực kéo quả nặng là: F = T – m2(g)sin(60) = T – 5(9.8)(.87) = T – 42.63.
- Gia tốc của 2 vật là bằng nhau, ta có (98 – T)/m1 = T – 42.63 /m2. Từ đó tính được T = 79.54 Newton.
{“smallUrl”:”https://www.wikihow.com/images_en/thumb/d/da/Calculate-Tension-in-Physics-Step-8-Version-2.jpg/v4-460px-Calculate-Tension-in-Physics-Step-8-Version-2.jpg”,”bigUrl”:”https://www.wikihow.com/images_en/thumb/d/da/Calculate-Tension-in-Physics-Step-8-Version-2.jpg/v4-760px-Calculate-Tension-in-Physics-Step-8-Version-2.jpg”,”smallWidth”:460,”smallHeight”:345,”bigWidth”:760,”bigHeight”:570,”licensing”:”<div class=”mw-parser-output”></div>”}
3
Trường hợp nhiều dây cùng treo một vật. Cuối cùng, hãy xét một hệ vật hình chữ “Y” – 2 sợi dây được buộc vào trần nhà đầu kia cột vào nhau và cùng cột với một dây thứ 3 và một đầu của dây thứ 3 đang treo quả nặng. Lực căng của sợi dây thứ 3 đã nằm ngay trước mặt chúng ta – Chỉ đơn giản là trọng lực, T = mg. Lực căng của 2 sợi dây 1 và 2 khác nhau và tổng lực căng của chúng phải bằng với trọng lực theo phương thẳng đứng và bằng không nếu theo phương ngang, giả sử hệ vật đang ở trang thái nghỉ. Lực căng mỗi dây bị tác động bởi khối lượng quả nặng và góc tạo bởi mỗi sợi dây với trần nhà.
- Giả thiết rằng hệ chữ Y của chúng ta đang treo qua nặng 10 kg, góc tạo bởi 2 sợi dây với trần nhà lần lượt là 30 độ và 60 độ. Nếu muốn tính lực căng mỗi dây, ta phải xét xem lực căng ngang và dọc của từng thành phần là bao nhiêu. Hơn nữa, 2 sợi dây này vuông góc với nhau, giúp ta phần nào dễ tính toán hơn bằng cách áp dụng hệ thức lượng trong tam giác:
- Tỷ số T1 hoặc T2 và T = m(g) lần lượt bằng với giá trị sin của các góc tạo bởi sợi dây tương ứng với trần nhà. Ta tính được T1, sin(30) = 0.5, và T2, sin(60) = 0.87
- Nhân lực căng dây của dây thứ 3 (T = mg) với giá trị sin của mỗi góc để tìm T1 và T2.
- T1 = .5 × m(g) = .5 × 10(9,8) = 49 Newton.
- T2 = .87 × m(g) = .87 × 10(9,8) = 85.26 Newton.
- Tỷ số T1 hoặc T2 và T = m(g) lần lượt bằng với giá trị sin của các góc tạo bởi sợi dây tương ứng với trần nhà. Ta tính được T1, sin(30) = 0.5, và T2, sin(60) = 0.87
- Nhân lực căng dây của dây thứ 3 (T = mg) với giá trị sin của mỗi góc để tìm T1 và T2.
- T1 = .5 × m(g) = .5 × 10(9,8) = 49 Newton.
- T2 = .87 × m(g) = .87 × 10(9,8) = 85.26 Newton.
xem thêm >> hoa sinh nhật, hoa khai trương, hoa chia buồn , điện hoa 24gio . shop hoa tươi , đặt hoa công nghệ
điên hoa 24gio , hoa tươi đẹp không tưởng, hoa tươi
Những câu nói hay, Đặt tên con ,Lời chúc sinh nhật
xem thêm >> hoa sinh nhật đẹp , lẵng hoa khai trương , điên hoa chia buồn , dien hoa
Hãy Goi Ngay ( Hoa Đẹp Rẻ Sang ) Giao Miễn Phí , Bạn Đang cần tìm shop hoa, hãy goi ngay shop nhé, nhận giao hoa tận nơi miễn phí, có hóa đơn vat, dịch vụ điện hoa chuyên nghiệp